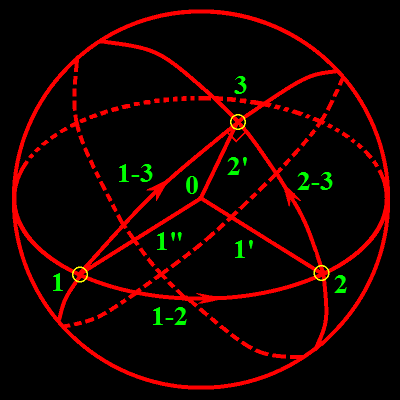
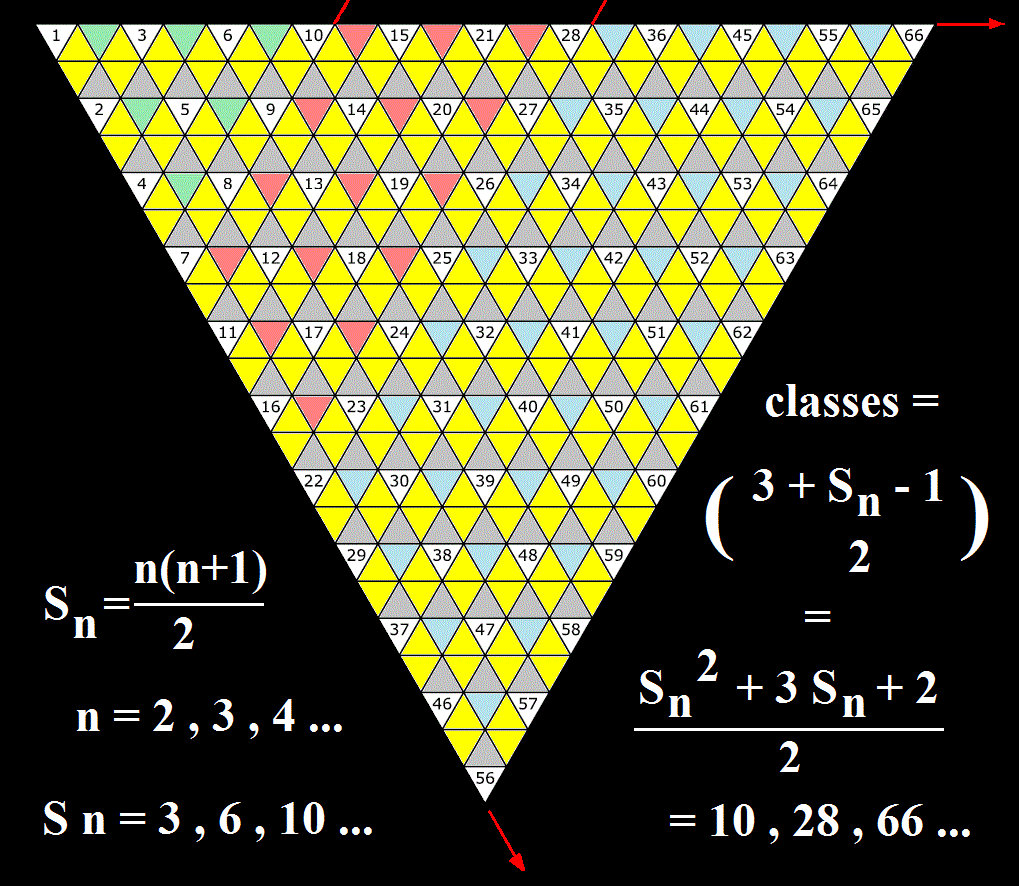
Números Triangulares denotado pela soma do conjunto natural.
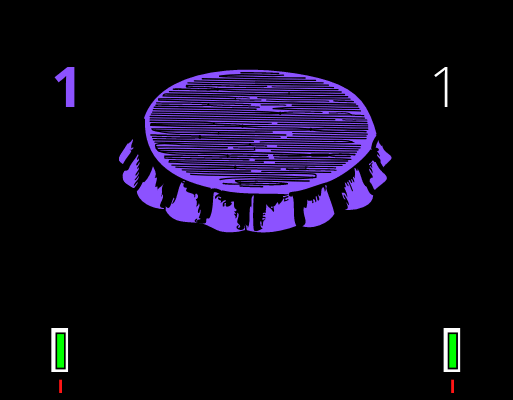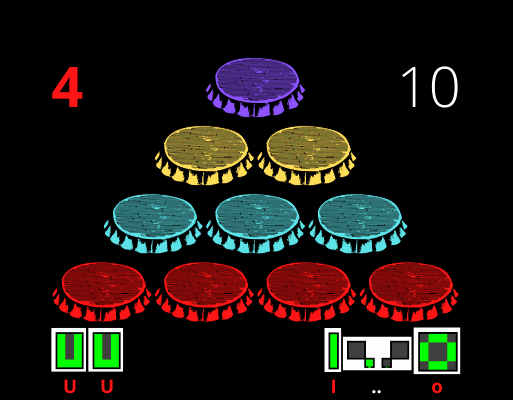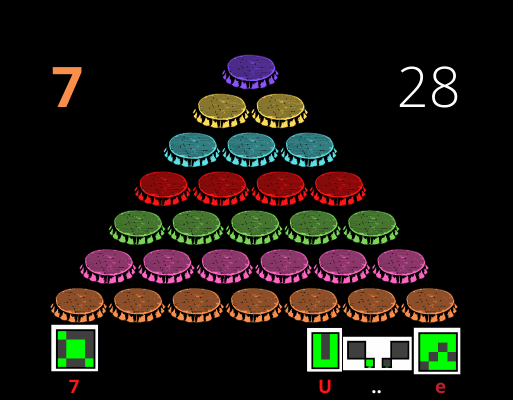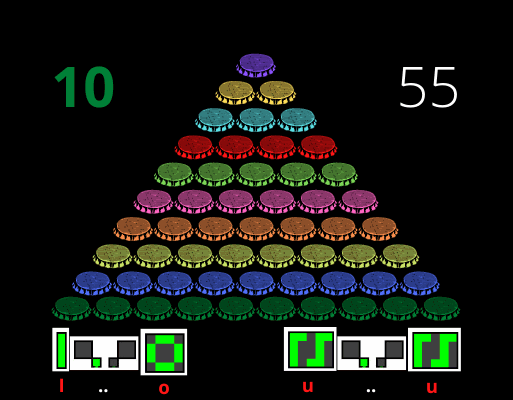
Soma de Gauss
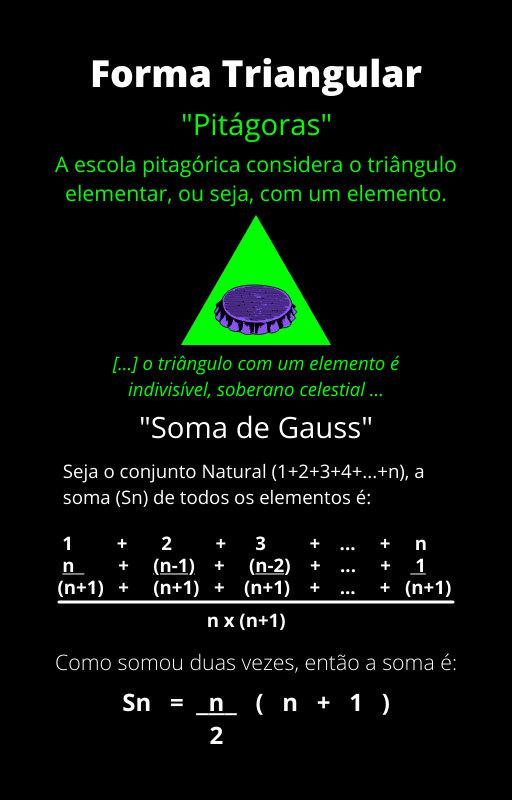
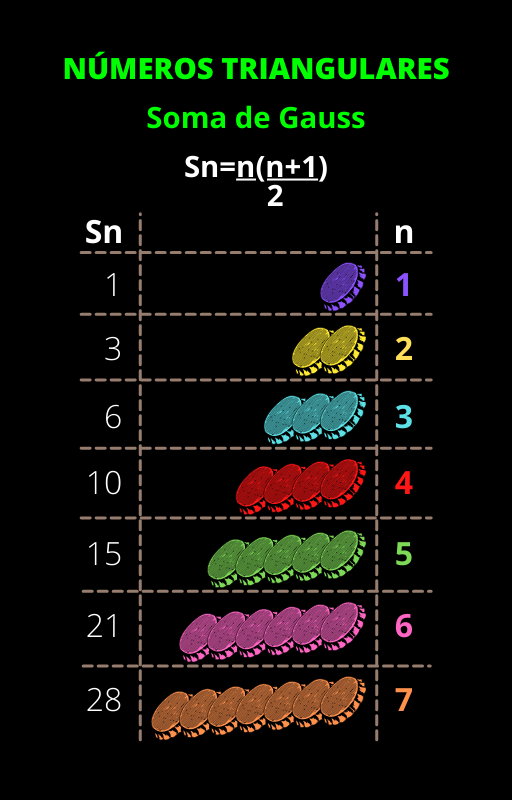
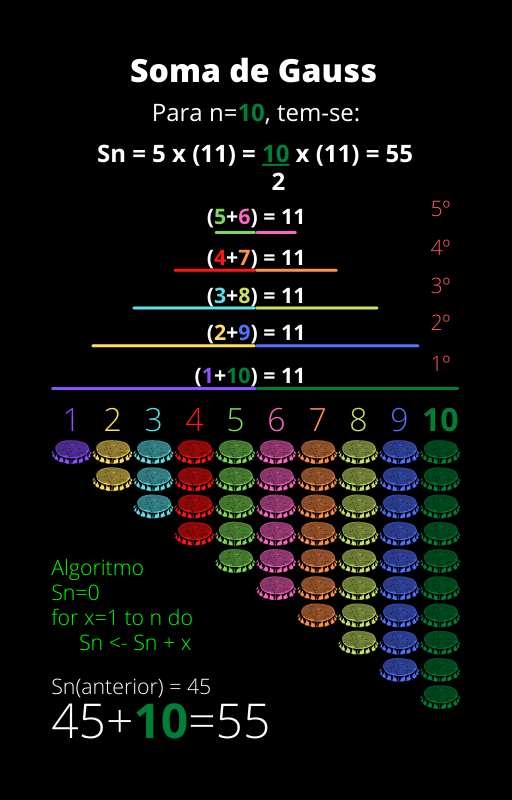
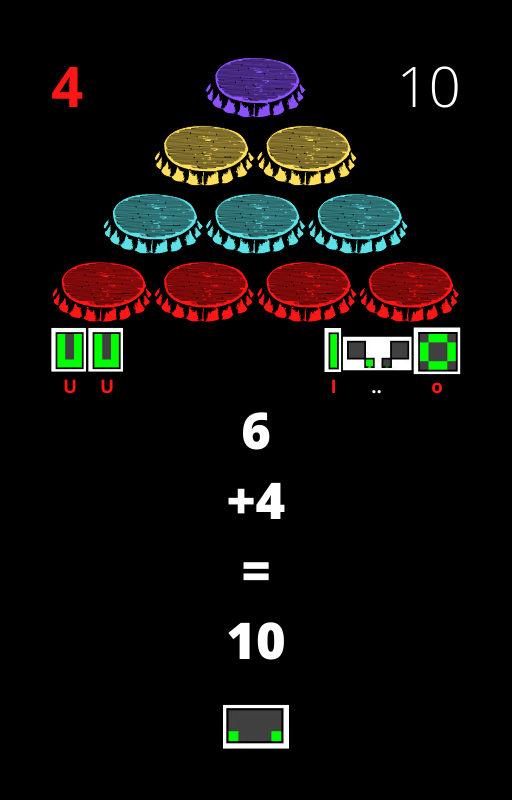
Para o conjunto dos números triangulares de Peirce, não considera o triângulo elementar, diferentemente da escola de Pitágoras. Ou seja, não existe o triângulo com um elemento, que denota como indivisível, soberano, Divino.
Introdução à divisão 3-tricotômica de signos
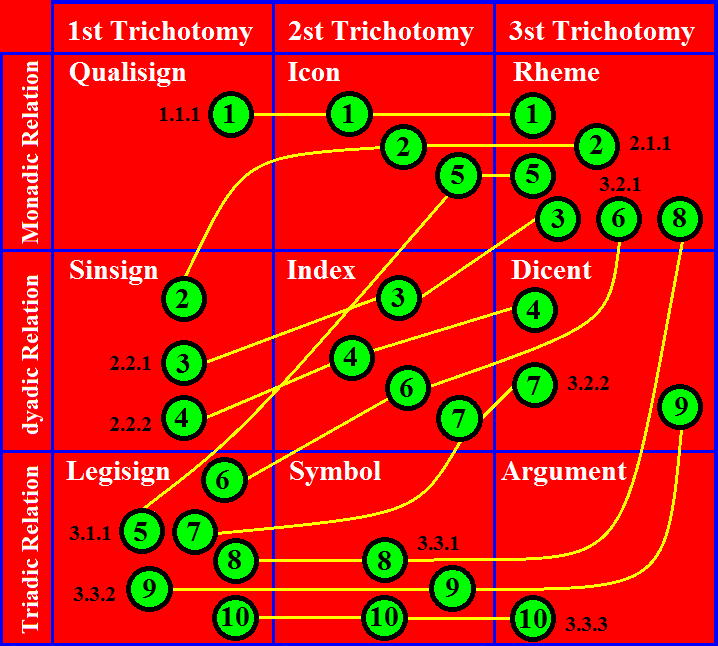
Segundo Savan (1987-88: 14), as combinações (cruzamentos) são permitidas peloque ele chama de “regra de qualificação”. Esta regra é a expressão de uma lei – praecisio(CP 1.353, 1.549, 2.428, 5.449), que chamarei de prescisão, e que permite aplicarrecursivamente classes de relações. Para nossos propósitos, prescisão é uma operação querestringe as possibilidades livres de combinação dos resultados das tricotomias. Astricotomias estão arranjadas conforme uma ordem de pressuposição, associada às categorias:caráter de apresentação (primeiridade) > caráter de representação (secundidade) > poderinterpretativo do signo (terceiridade). O tipo de relação que responde à primeira questão qualifica, ou especifica, a segunda que qualifica a terceira (Savan 1987-88: 14). De acordocom esta regra, um “primeiro [relação monádica] pode ser qualificado apenas por umprimeiro [relação monádica]; um segundo [relação diádica] pode ser qualificado por umprimeiro [relação monádica] e por um segundo [relação diádica]; um terceiro [relaçãotriádica] pode ser qualificado por um primeiro [relação monádica], por um segundo [relaçãodiádica] e por um terceiro [relação triádica]” (Savan ibid.). Ainda de acordo com Savan(ibid.), “a ‘regra de qualificação’ estipula que, em qualquer sucessão, um membro de umacategoria pode ser seguido por um membro de uma categoria de igual ou menor valor —um primeiro pode ser qualificado apenas por um primeiro; um segundo pode ser qualificadopor um primeiro e por um segundo; um terceiro pode ser qualificado por um primeiro,segundo, ou terceiro”. Esta regra, que em Deledalle (apud Jappy 1984: 16) aparece como“princípio hierárquico cenopitagórico”, eem Tursman (1987: 38) como “restrição de ligaçãofaneroquímica”, é usada para obter classes de relações n-tricotômicas: 10 classes, 28 classese 66 classes de signos.
(Queiroz,2004) [20]
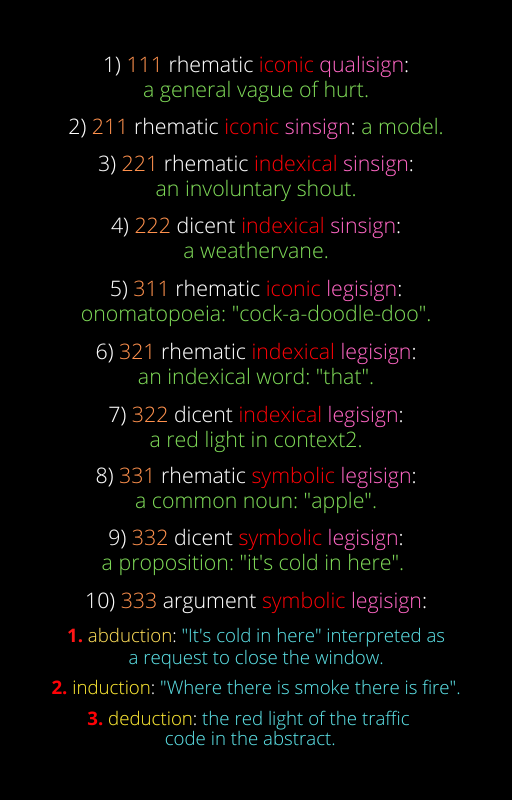
As dez combinações (classes), ou cruzamentos, baseadas em três tricotomias, quedevem satisfazer as “regras de qualificação” são: 111, 211, 221, 222, 311, 321, 322, 331,332, 333.
(I) 111, ou qualisigno, é uma “qualidade” que é um signo; relativamente a sua própria natureza é uma primeiridade. Assim, só pode ter um ícone como objeto, e um rema como interpretante — uma “sensação de vermelho” (CP 2.254).
(II) 211, ou um sinsigno icônico, é um evento, ou ocorrência (como todo sinsigno), que é um signo; é uma secundidade quanto a sua própria natureza. Seu objeto é um ícone, que ele interpreta como um rema — um “diagrama particular” (CP 2.255).
(III) 221, ou sinsigno indexical remático, é uma ocorrência que é um signo, que está para seu objeto, também uma ocorrência, através de um rema (signo de possibilidade) — “um grito espontâneo” (CP 2.256).
(IV) 222, ou sinsigno indexical dicente, é um signo que é uma ocorrência, e que é interpretado como realmente afetado por seu objeto, também uma ocorrência — um “catavento”(CP 2.257).
(V) 311, ou legisigno icônico, é uma lei que é signo, e cujo objeto é uma possibilidade —um “diagrama à parte sua individualidade” (CP 2.258).
(VI) 321, ou legisigno indexical remático, é uma lei que é signo, e que está para seu objeto, que é uma ocorrência, através de uma possibilidade — um “pronome demonstrativo” (CP 2.259).
(VII) 322, ou legisigno indexical dicente, é uma lei que é signo, e que está para seu objeto, uma ocorrência, através de uma conexão de fato — um “pregão de mascate” (CP2.260).
(VIII) 331, legisigno simbólico remático, é uma lei que está para um objeto da mesma natureza através de uma possibilidade — um “substantivo comum” (CP 2.261).
(IX) 332, ou legisigno simbólico dicente, é uma lei, interpretada como estando para um objeto da mesma natureza através de uma conexão de fato — é uma “proposição ordinária” (CP 2.262).
(X) 333, ou legisigno argumental simbólico, é uma lei, e representa um objeto da mesma natureza como uma lei — “argumento” (CP 2.263).
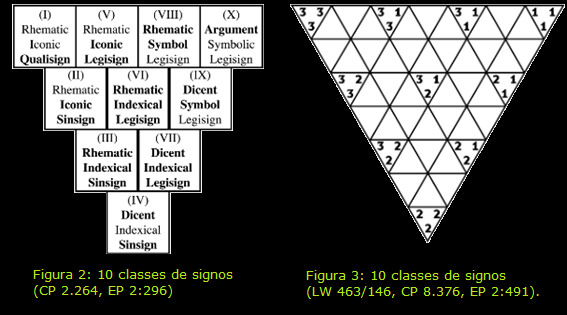
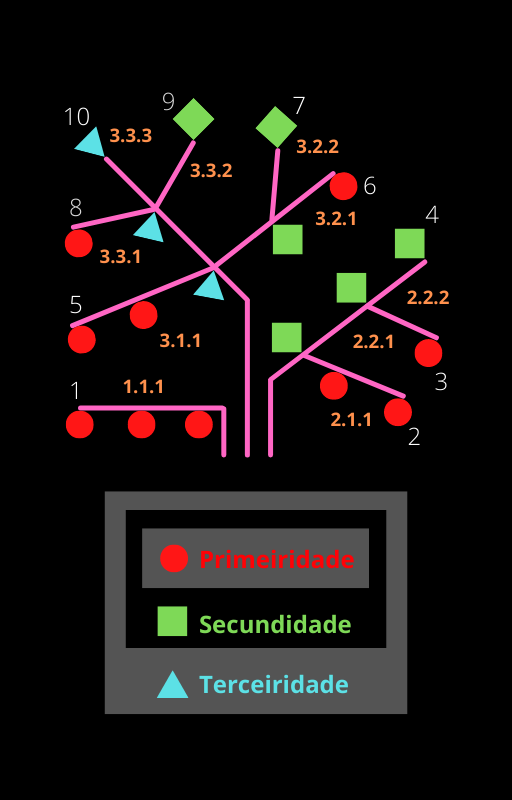
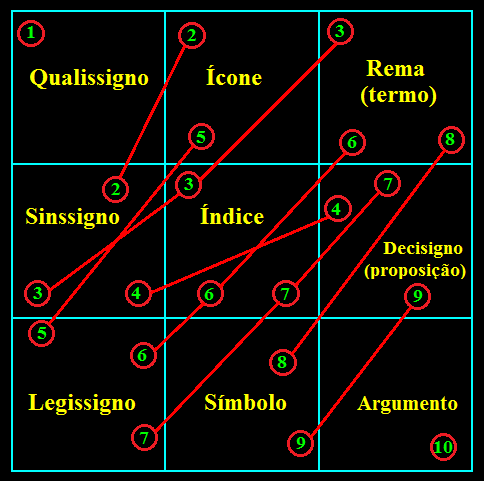
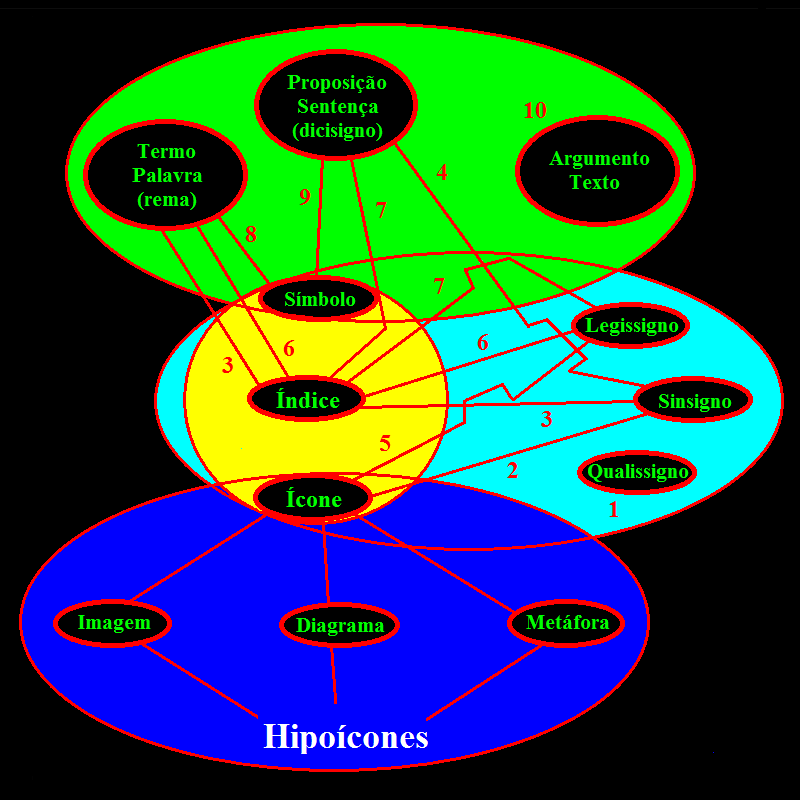
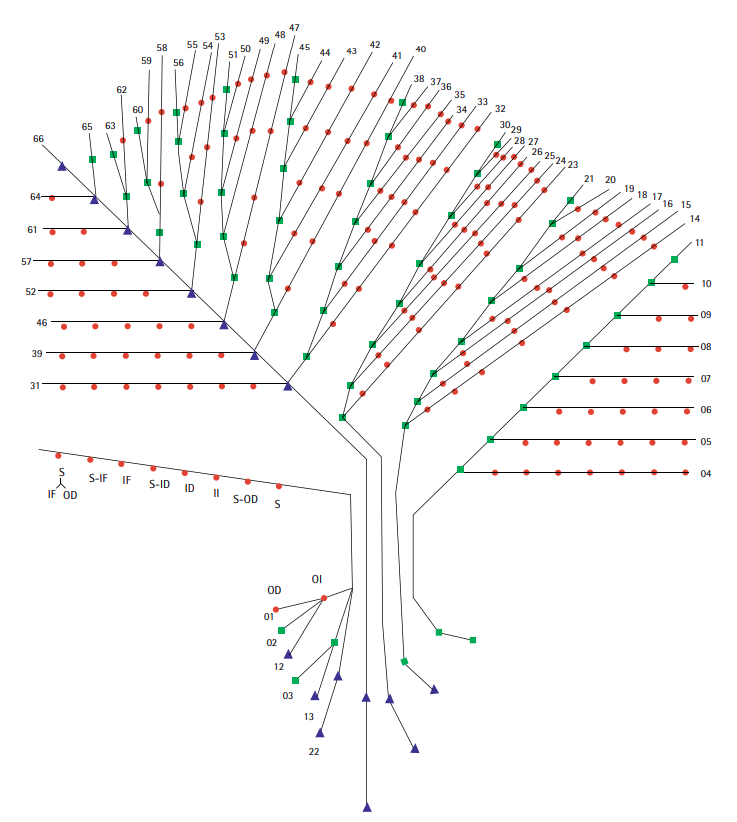
Peirce propôs dois modelos gráficos para representar as dez classes de signos (figuras2 e 3). Eles podem ser chamados de “diagramas de relações periódicas”, ou de “relações de afinidade”, entre classes de signos e baseiam-se em “taxas” de proximidade relativas entre suas partes. Figura 2: 10 classes de signos (CP 2.264, Figura 3: 10 classes de signos (LW 463/146,EP 2:296).CP 8.376, EP 2:491).
(Queiroz,2004) [20]
Mensagens Cifradas: a construção de linguagens diagramáticas
Quando a linguagem verbal materializa-se em formas de escrita, ela adquire características particulares do sistema de linguagem visual. Torna-se, então, necessário investigar o poder significativo das formas visuais em textos verbais. A visualidade do sistema de escrita verbal agrega duas funções da escrita: a comunicativa e a poética visual. A função comunicativa caracteriza o sistema verbal, estando também presente na linguagem verbal oral. Já a função poética visual é particular aos sistemas escrita, sendo expressa pela caligrafia manual e pela tipografia.
(Borges, 2010) [21]
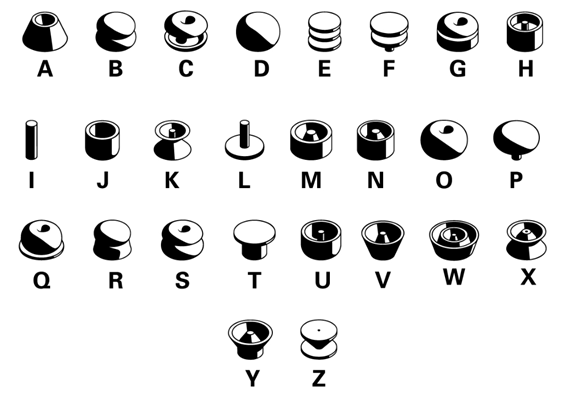
l typefaces for Latin alphabet are designed to be used for the conventional left-to-right reading direction. WENS was designed for reading and writing in four directions.
JI LEE

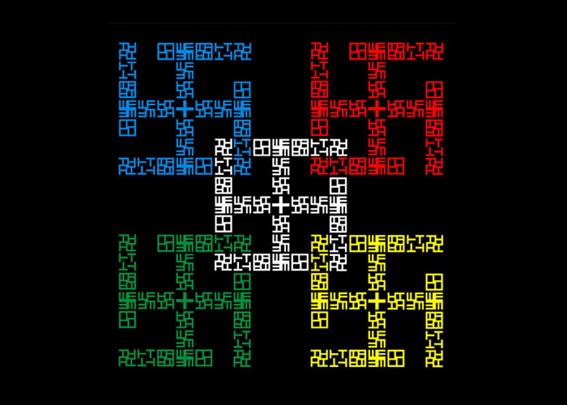
Univers Revolved: A Three-Dimensional Alphabet (2004)
JI LEE
Univers Revolved — A 3D Alphabet
JI LEE